函数的水平渐近线怎么求

在数学的世界里，函数是语言，而水平渐近线就像是这门语言中的助词，它为函数图像提供了新的视角和解读。今天，我们就一起探索如何求解函数的水平渐近线。

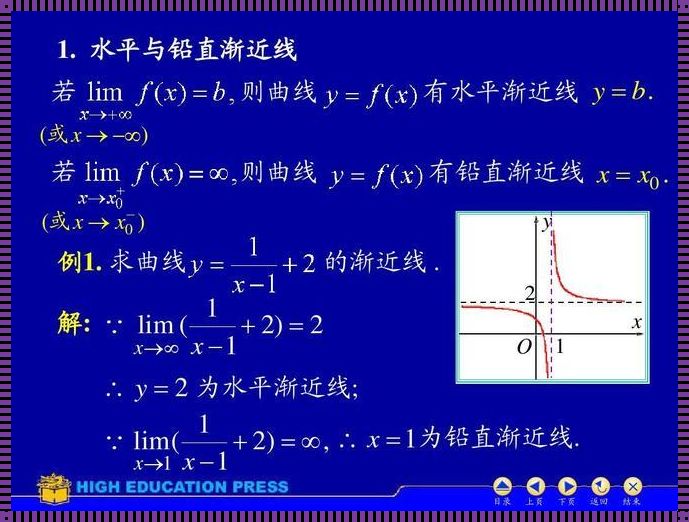
首先，我们需要理解什么是水平渐近线。水平渐近线是指当x趋于正无穷或负无穷时，函数图像与x轴趋于平行的直线。换句话说，它是函数图像在无限远处的“轮廓”。

求解水平渐近线的方法主要有两种：

方法一：直接观察法 对于一些简单的函数，如多项式函数或者有理函数，我们可以通过直接观察函数的表达式来确定水平渐近线。

例如，考虑函数f(x) = 2x + 3，这是一个一次函数。由于系数2是正数，函数图像是一条斜率为正的直线。无论x取值多大或多小，函数值f(x)都会随着x的增大而无限增大。因此，这条函数的图像会无限接近x轴，即水平渐近线为y=0。

方法二：极限分析法 对于更复杂的函数，如指数函数、对数函数或者分段函数，我们可能需要使用极限的方法来求解水平渐近线。

步骤一：计算极限lim(x→∞)f(x)和lim(x→-∞)f(x)。 步骤二：如果这两个极限存在且相等，那么这个值就是水平渐近线。

例如，考虑函数f(x) = (1/x)^2，这是一个分段函数。我们可以分别计算x趋向正无穷和负无穷时的极限。当x趋向正无穷时，(1/x)^2趋向0；当x趋向负无穷时，(1/x)^2同样趋向0。因此，水平渐近线为y=0。

通过这两种方法，我们就能求解出函数的水平渐近线。然而，需要注意的是，并非所有的函数都有水平渐近线。例如，函数f(x) = 1/x就没有水平渐近线，因为它在x趋向正无穷和负无穷时，函数值会交替地在0上下震荡。

在探索数学的世界时，我们不仅要关注函数的局部特性，如极值和拐点，也要理解它们的整体行为，比如水平渐近线。这不仅能帮助我们更好地理解函数的本质，还能为实际应用提供指导。无论是在工程、物理还是经济学领域，理解函数的水平渐近线都有助于我们预测和控制系统的长期行为。

在这个探索过程中，我们像侦探一样，通过观察、分析和推理，揭示了函数图像的秘密。数学，这个富有无穷奥秘的领域，正等待着我们用智慧和勇气去进一步探索。